1. 图解排列组合

继续图解AMC系列之排列组合

2. 1 测试能力

上来先看5道典型排列组合题目，看看各位能正确做出几道题目（答案我放在了文章末尾）

1、有六本不同的书，其中四本是英语书，两本是中文书，在这六本书中任选两本中文书和两本英文书，每周看一本，但是要求连续四周看完，共有多少方法？

2、ABCDEFG七位同学在操场排成一列，其中学生B与C必须相邻。请问共有多少方法？

3、将三盘同样的红花和四盘同样的黄花摆放成一排，要求三盘红花互不相邻，共有多少种方法？

4、将5件不同的奖品全部奖给3个学⽣,每⼈⾄少⼀件奖品,则不同的获奖情况种数是一共有多少种方法？

5、12个小球放到3个不同的盒子里，每个盒子至少1个小球，共有多少种方法？

排列组合的题目非常烧脑，哪怕一道题目都不能解答也都很正常。当前上班族的逻辑思维都应付在了客户应酬、代码复制黏贴、办公室文化等

因此针对上述各种题型的排列组合，希望能够找到一种行之有效的方法论，不管题型如何调整，都能够以不变应万变的策略快速找到突破口

3. 2 方法推导

3.1 2.1 有序和无序

首先我们先看一道最基本的题型

10个同学选出3个人，去坐3个位置，有多少种不同的坐法？10个同学里选出3个不同的同学有多少种方法？

简单解法：事件发生的概率基本按照分类按加法、分步按乘法的方式。第一步先站在位置角度，需要从10个同学里选一个出来，那么第一个位置有10种坐法，然后剩下9个同学在等位置，第二个位置就有9种坐法，以此类推，第三个位置有8种坐法。因此总的坐法就是分步相乘，即10*9*8=720种坐法。而至于第二个问，我们先暂时先不直接求解。

引申概念：

1、有序的坐法：从题目本身来看，这种场景下坐的位置是有顺序讲究的，如果我们给同学编号，123和312是不同的坐法，即同一个同学坐在第一个位置和坐在第三个位置是不一样的坐法

2、无序的选择：从10个同学里选出3个同学，而不去坐位置，只是待排序。这种场景下选择是无序的，如果我们给同学编号，同样是选出1、2、3三名同学，先选1号还是先选3号，本质都是一样的

3.2 2.2 排列和分组

公式解法：

1、排列数【有序】：我们根据简单解法中分步相乘的方法，即10*9*8=720种坐法记为$$A_{10}^{3}$$因此今后类似有多少个不同的人去坐多少个位置，就是求排列数A的值

2、组合数【无序】：针对第二个问题，我们把从10个同学里选择3个同学，我们记为$$C_{10}^{3}$$我们这里做个简单公式推导，我们将题述10个同学选出3个人，去坐3个位置，有多少种不同的坐法?分解为两个动作

①先从10个同学里选出3个同学

②然后让这3个同学去坐三个不同位置

三个同学去坐三个不同位置，解法是：$$A_{3}^{3}$$因此根据分步相乘的理论，得出公式为：$$A_{10}^{3}=C_{10}^{3}\times A_{3}^{3}$$因此组合数C的计算公式就等于$$C_{10}^{3}=A_{10}^{3}{\div} A_{3}^{3}$$因此今后类似有多少个不同的人去选择多少种组合，就是求组合数C的值

3.3 2.3

凡是从n个不同的物品/人物选择出m个来，是一种无序的选择英文正好是Choose就是组合数，公式为$$C_{n}^{m}$$凡是从n个不同的物品/人物去按顺序去坐m个位置或者按顺序去排列英文正好是arrange就是排列数，公式为$$A_{n}^{m}$$

注意n是大于等于m的

排列有序，组合无序

4. 3 分层的思考方法

我们希望找到一种统一的解题思路，不仅可以应对简单诸如多少人去坐多少位置的题目，还可以针对文章开始题目1这种类型

针对题目1有六本不同的书，其中四本是英语书，两本是中文书，在这六本书中任选两本中文书和两本英文书，每周看一本，但是要求连续四周看完，共有多少方法？

我们把六本书作为原始层，是需要待选择的，经过选择后进入选择成，进行待排列状态，最终根据位置的数量进行最终层完成排列

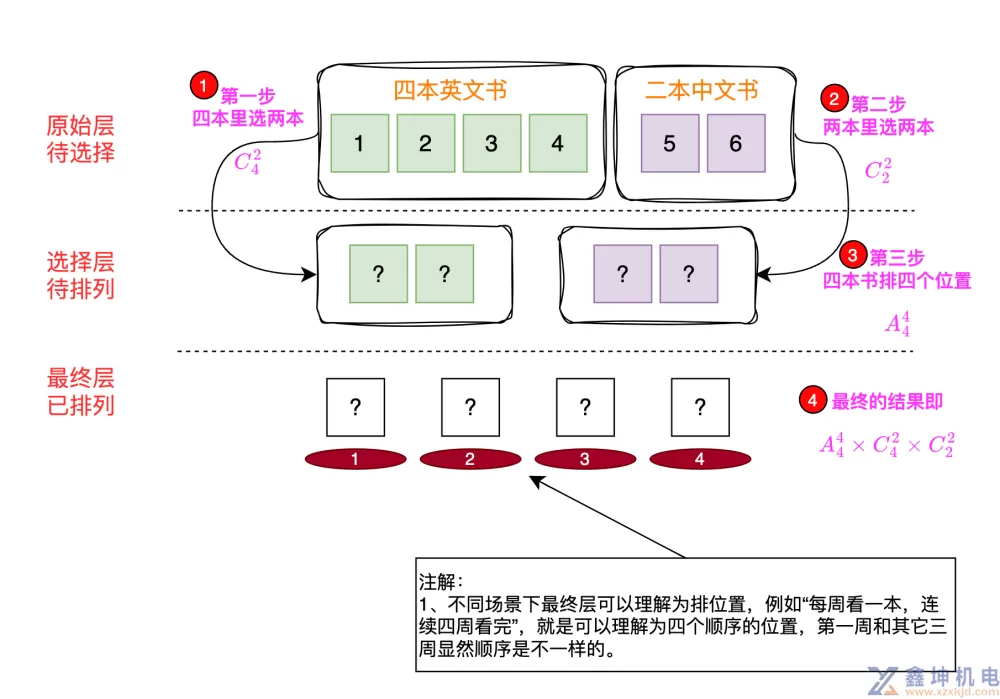
有了这个分层思考的解题思路，我们再看开头的第一道题目

某小组有10个人，从中选出两个人去参加劳动，有多少种选法？

很明显，答案直接使用组合公式$$C_{10}^{2}=45$$如果选出两个人，一个人去扫地，一个人去擦窗，有多少种不同的选法？$$C_{10}^{2}\times C_{2}^{1}\times C_{1}^{1}=90或者A_{10}^{2}=90$$

这里注意这里，归属于扫地和擦窗，本质上还是分类，属于选择层的概念，并不是去按顺序排位置，因此是使用组合的公式

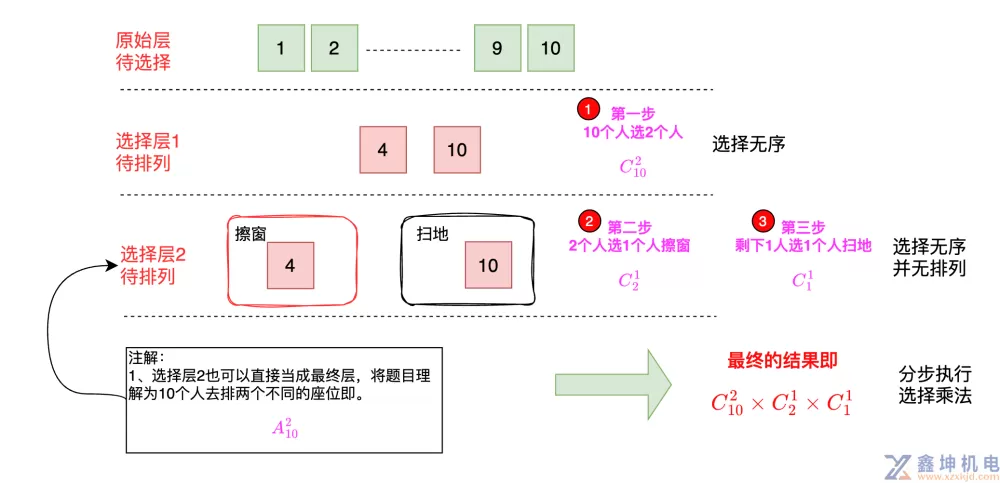
如果选出五个人，两个人擦窗，三个人扫地，有多少种不同选法？$$C_{10}^{5}\times C_{5}^{3}\times C_{2}^{2}=2520$$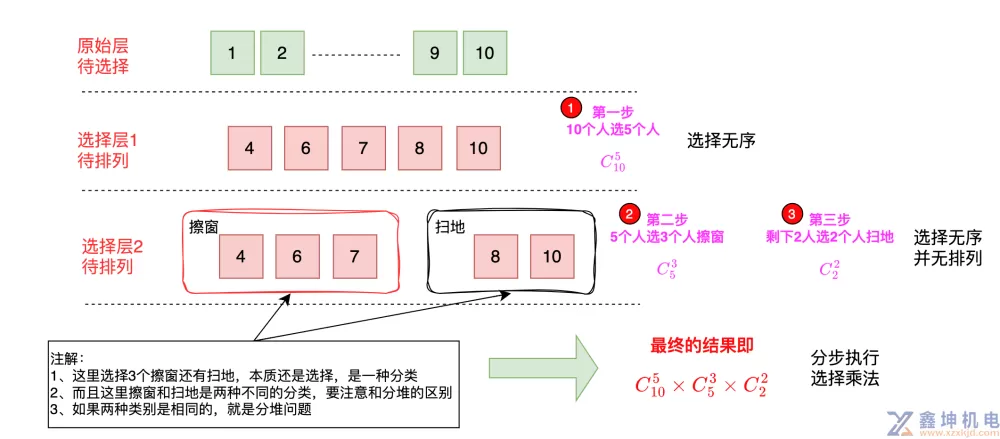

就像图中所示的注解：

1、这里选择3个擦窗还有扫地，本质还是选择，是一种分类

2、而且这里擦窗和扫地是两种不同的分类，要注意和分堆的区别

3、如果两种类别是相同的，就是分堆问题

4.1 3.1 变种一之分堆

重要：如何选择进相同的容器则为分堆，分堆问题重点是要去做重计算

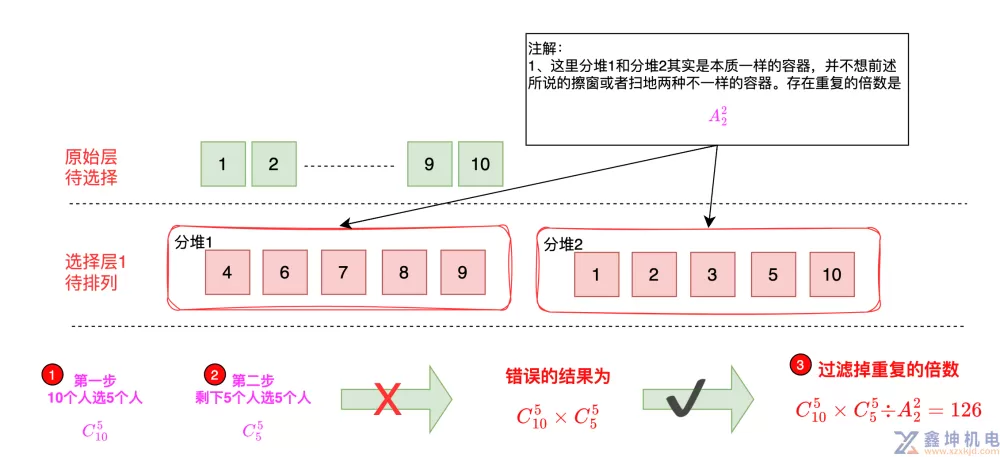
如果把这10个人分成两队，每队5人，进行拔河比赛，一共有多少种不同分法？

如果还是按照前面选择层的方式，则最终结果计算错误，原因是进行了重复计算

重复计算的本质如图所示：

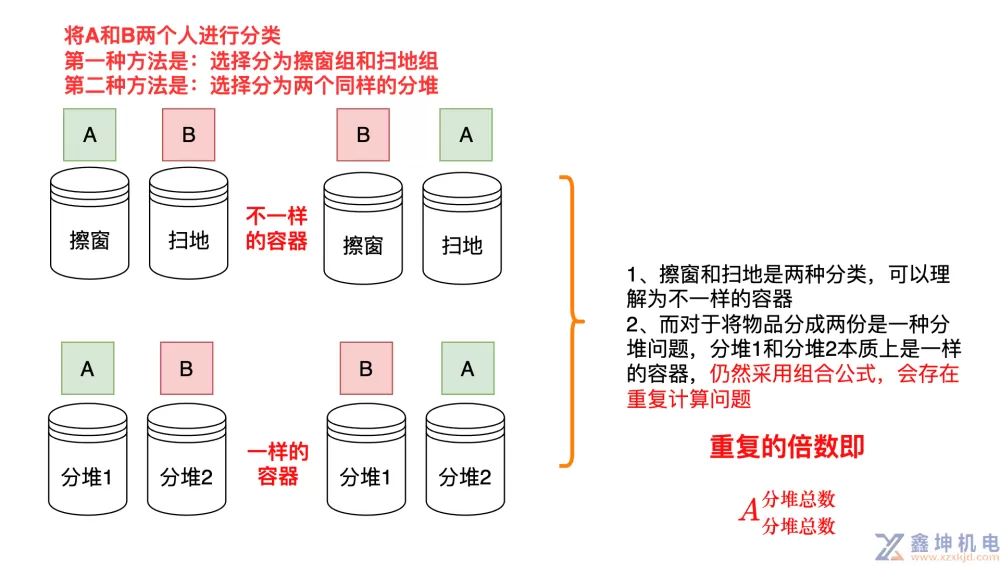
因此我们需要在原来分层思考的方法上进行调整，即变种一之分堆问题，重点是要过滤重复的数

4.2 3.2 变种二之打包法

我们再来看看开头题目2ABCDEFG七位同学在操场排成一列，其中学生B与C必须相邻。请问共有多少方法？

将B和C进行打包，这样就变成了6个人去坐6个位置

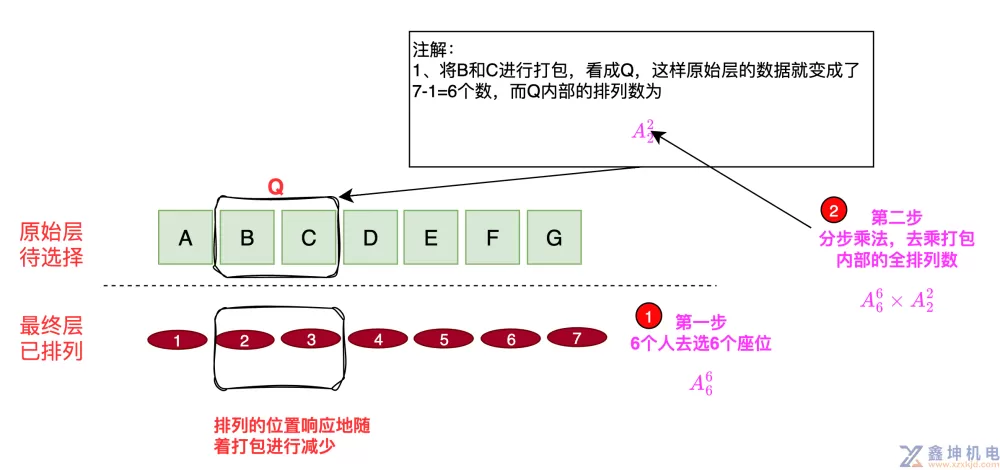
$$A_{6}^{6}\times A_{2}^{2}=1440$$

4.3 3.3 变种三之插空法

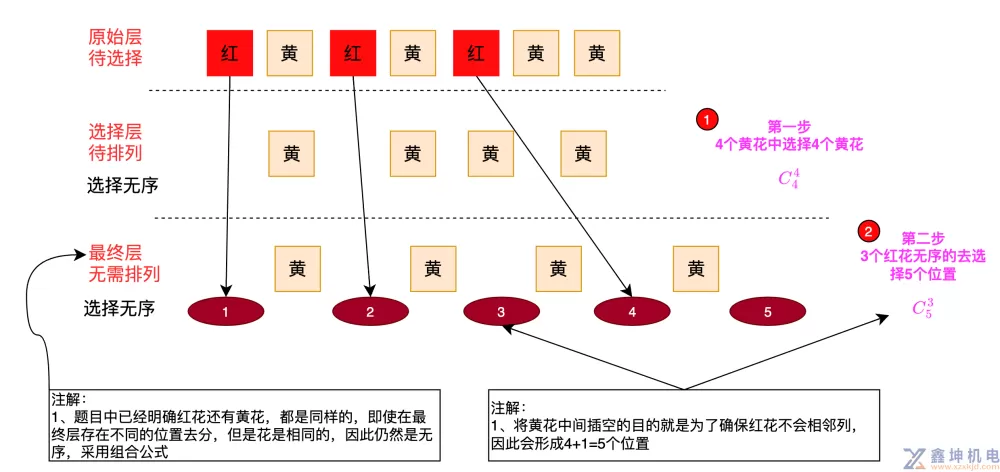
我们再来看开头题目3将三盘同样的红花和四盘同样的黄花摆放成一排，要求三盘红花互不相邻，共有多少种方法？

对于这种要求互不相邻的要求，就是要将另外一方先排序后再进行插空排序

注意：虽然上一句中使用了排序的字眼，但是排序的对象花朵每个都一样，因此仍然是组合的公式，这点是关键

4.4 3.4 变种四之综合考虑法

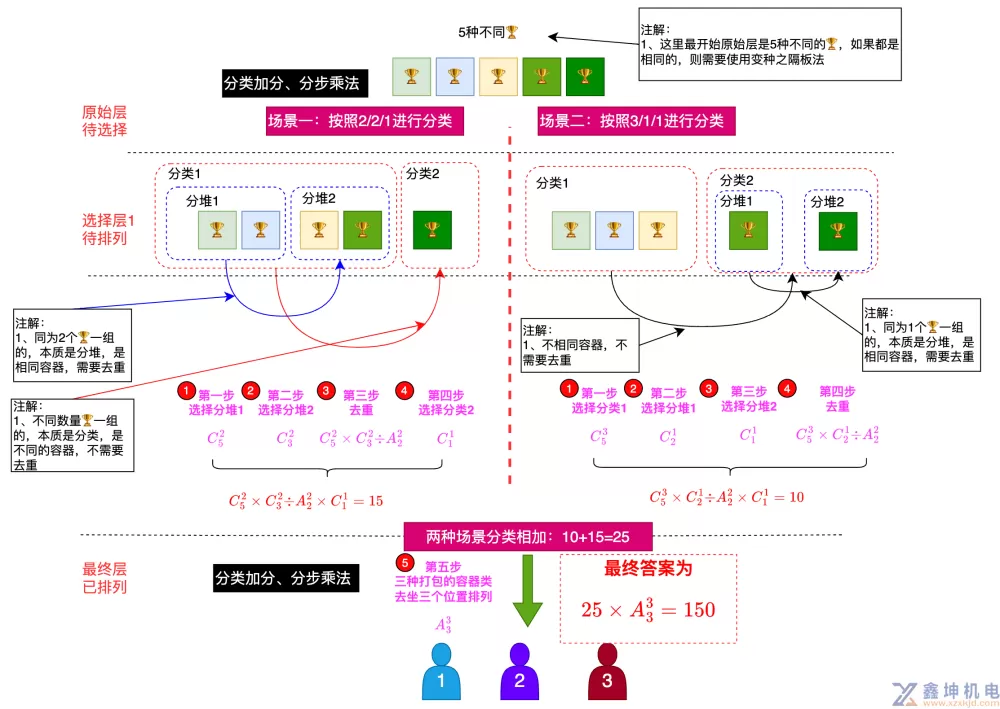
我们再来看开头题目4将5件不同的奖品全部奖给3个学⽣,每⼈⾄少⼀件奖品,则不同的获奖情况种数是一共有多少种方法？

针对开始的奖品，是不同的前提下使用这种综合考虑

综合考虑到分类加法原理与分步乘法原理的使用

我们将奖杯分成2/2/1三种容器和3/1/1三种容器，容器看成奖杯的打包，然后颁发给三个学生，三个学生是不一样，有顺序的，因此最后是一个排列的公式

重点是针对容器内相同个数的奖杯的分类，则看成是有重复计算的分堆计算，需要做去重计算

4.5 3.5 变种五之隔板法

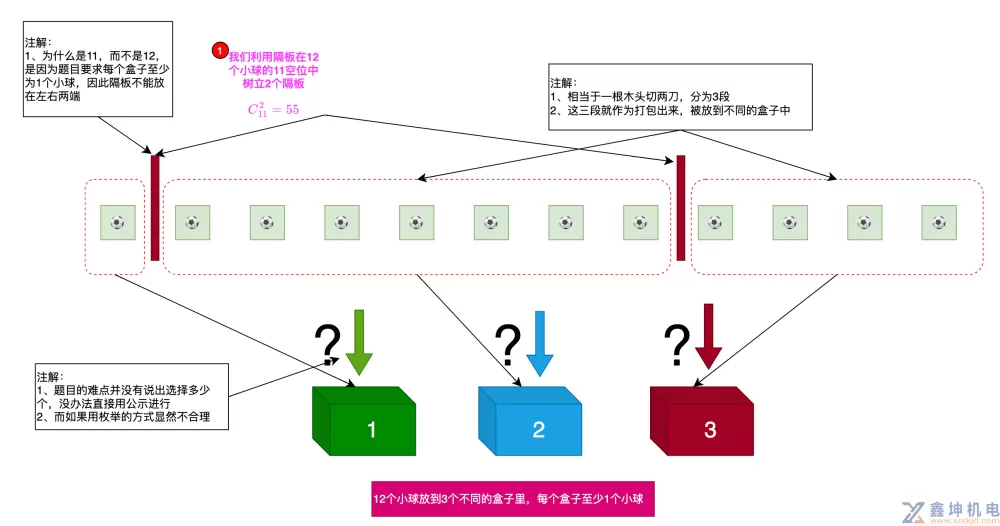
最后我们再看下第5题12个小球放到3个不同的盒子里，每个盒子至少1个小球，共有多少种方法？

题目的难点并没有说出选择多少个，没办法直接用公示进行

而如果用枚举的方式显然不合理

我们换个思路去考虑：相当于一根木头切两刀，分为3段，这三段就作为打包出来，被放到不同的盒子中

就是11个空位去选择2个，没有顺序问题，因此是

为什么是11，而不是12，是因为题目要求每个盒子至少为1个小球，因此隔板不能放在左右两端

$$C_{11}^{2}=55$$

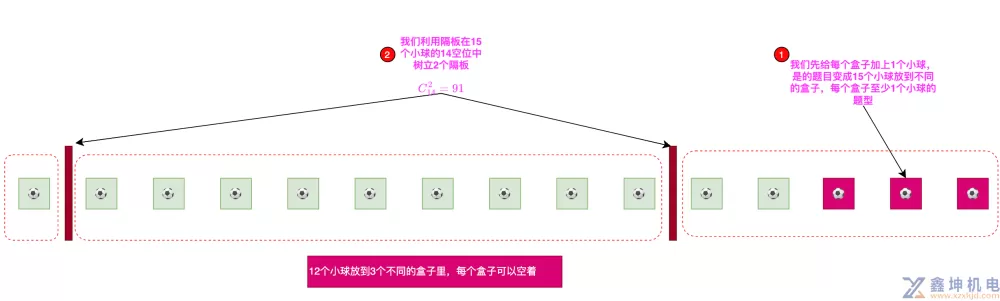
这里还有一种变种

就是题目可以这么问12个小球放到3个不同的盒子里，每个盒子可以空着,有多少种方法

其实可以反过来思考，先加3个小球，使得题型变成隔板法的标准题型

文章末尾答案

1、题目1答案：144种

2、题目2答案：1440种

3、题目3答案：10种

4、题目4答案：150种

5、题目5答案：55种