一图三例说明白贝叶斯公式
1. 1 一张图解释贝叶斯公式
英国数学家托马斯:贝叶斯( Thomas Bayes),在1763年发表的一篇论文中,首先提出了这个定理
贝叶斯在他的文章中是为了解决一个“逆概率”的问题
贝叶斯公式能够在有限的信息下,帮助我们预测出概率
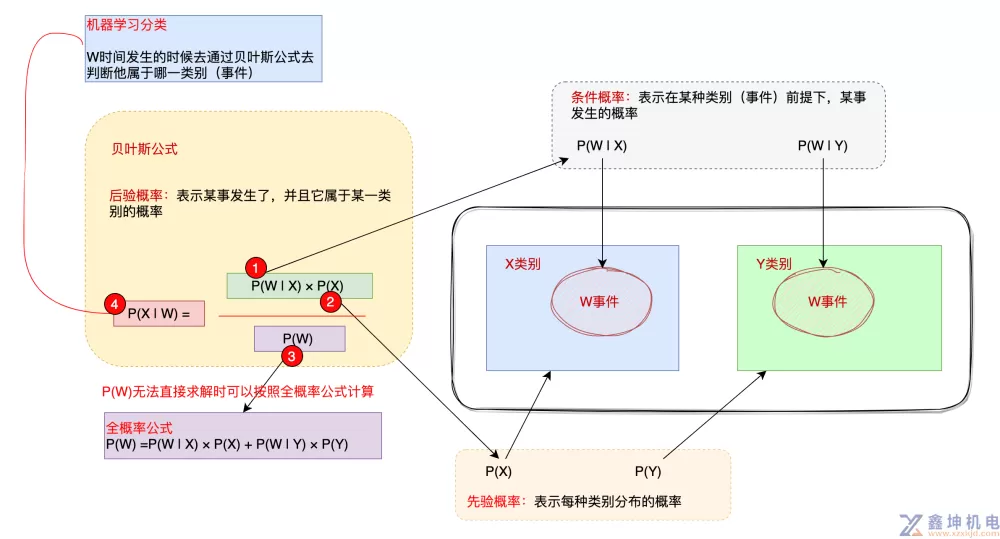
条件概率表示在某种类别(事件)前提下,某事发生的概率
只要在题设条件中有:**”已知事件A发生”** 或“在事件B发生的条件下〞等,均要考虑条件概率,条件概率帮助我们考虑问题时限在正确的可能性(条件)下
先验概率表示每种类别分布的概率
2. 2 三个示例
2.1 2.1 示例1
大年三十晚上,爷爷奶奶发红包。爷爷准备的红包是 4 个 50 元的,6 个 100 元的。奶奶准备的红包是 8 个 50 元的,4 个 100 元的。全家人随机抽,你运气很好,拿到一个 100 元的红包。请问这个红包来自爷爷的概率有多少?来自奶奶的概率有多少?
解答
爷爷一共10个红包,奶奶一共12个红包
分类(事件A)爷爷的概率是P(爷爷) = 10个红包/22个红包=5/11
分类(事件B)奶奶的概率是P(奶奶) = 12个红包/22个红包=6/11
分类(事件A)爷爷条件下(或者理解:范围下),抽中100元红包的概率是=6个红包/10个红包=3/5。这里分母10个红包指得是爷爷一共10个红包
分类(事件B)奶奶条件下(或者理解:范围下),抽中100元红包的概率是=4个红包/12个红包=2/6。这里分母12个红包指得是奶奶一共12个红包
注意:这里全概率P(100)是直接可以求的,不需要全概率公式:P(100)=10个100元红包/22个总红包=5/11【有些时候全概率需要使用全概率公式计算】
根据贝叶斯公式,其实就是求发生了一个事件(抽到了1个100元的红包)来自爷爷还是奶奶的概率
即通过先验概率(爷爷和奶奶分类的全概率)、条件概率(爷爷或奶奶类别或者范围下100元红包的条件概率)得出后验概率(他属于哪个类别(爷爷或奶奶)的概率是多少)
P(爷爷 | 100) = P(100 | 爷爷) × P(爷爷)/ P(100) = (3/5) × (5/11) ÷ (5/11) = 3/5
P(奶奶 | 100) = P(100 | 奶奶) × P(奶奶)/ P(100) = (2/6) × (6/11) ÷ (5/11) = 2/5
| 分析内容 | 分类(事件A)爷爷 | 分类(事件B)奶奶 |
|---|---|---|
| P(W) 先验概率 每种类别的概率 | 5/11 | 6/11 |
| 条件概率 在各分类中某事件的概率 | 3/5 | 2/6 |
| 全概率 某种程度上可以理解先分类再分步 | 5/11(全局均是这个值) | 5/11(全局均是这个值) |
| 后验概率,发生某事件条件下属于这个类别的概率 | 3/5 | 2/5 |
2.2 2.2 示例2
在夏季,某公园男性穿凉鞋的概率为1/2,女性穿凉鞋的概率为2/3,并且该公园中男女比例通常为2:1
若你在公园中随机遇到一个穿凉鞋的人,请问他的性别为男性或女性的概率分别为多少?
解答
分类(事件A)男性的概率是P(男性) = 2/3
分类(事件B)女性的概率是P(女性) = 1/3
分类(事件A)男性条件下(或者理解:范围下)穿凉鞋的概率,即条件概率P(凉鞋 | 男性)=1/2
分类(事件B)女性条件下(或者理解:范围下)穿凉鞋的概率,即条件概率P(凉鞋 | 女性)=2/3
注意这里与示例1不一样的地方是,对于全概率是没办法直接求出的,因此利用全概率公式
全概率公式
P(凉鞋) = P(男性) × P(凉鞋 | 男性) + P(女性) × P(凉鞋 | 女性) = 2/3 × 1/2 + 1/3 × 2/3= 5/9
P( 男性 | 凉鞋) = P(凉鞋 | 男性) × P(男性)/ P(凉鞋) = (1/2) × (2/3) ÷ (5/9) = 3/5
P( 女性 | 凉鞋) = P(凉鞋 | 女性) × P(女性)/ P(凉鞋) = (2/3) × (1/3) ÷ (5/9) = 2/5
| 分类(事件A)男性 | 分类(事件B)女性 | |
|---|---|---|
| P(W) 先验概率 每种类别的概率 | 2/3 | 1/3 |
| 条件概率 在各分类中某事件的概率 | 1/2 | 2/3 |
| 全概率 某种程度上可以理解先分类再分步 | 5/9(全局均是这个值) | 5/9(全局均是这个值) |
| 后验概率,发生某事件条件下属于这个类别的概率 | 3/5 | 2/5 |
2.3 2.3 示例3
某学校组织学生进行答题比赛,已知共有4道A类试题,8道B类试题,12道C类试题,学生从中任选1道该题作答,学生甲答对A,B,C这3类试题的概率分别是1/2,1/4,1/6,若甲答对所选试题,则这道题是B类试题的概率为【2023春 重庆-高二校联考期中】
解答
分类(事件)总和为4+8+12=24
分类(事件A)A类试题的概率是P(A类试题) = 1/6
分类(事件B)B类试题的概率是P(B类试题) = 1/3
分类(事件C)C类试题的概率是P(C类试题) = 1/2
分类(事件A)答A类试题条件下(或者理解:范围下)答对所选试题的概率,即条件概率P(答对 | A类试题)=1/2
分类(事件B)答A类试题条件下(或者理解:范围下)答对所选试题的概率,即条件概率P(答对 | B类试题)=1/4
分类(事件C)答A类试题条件下(或者理解:范围下)答对所选试题的概率,即条件概率P(答对 | C类试题)=1/6
同样的,对于全概率是没办法直接求出的,因此利用全概率公式
全概率公式
P(答对) = P(A类试题) × P(答对 | A类试题) + P(B类试题) × P(答对 | B类试题) + P(C类试题) × P(答对 | C类试题)= 1/4
直接使用贝叶斯公式
算“逆概率”即“答对所选试题,则这道题是B类试题的概率“
P( B类试题 | 凉答对) = P(B类试题) × P(答对 | B类试题) / P(答对)= (1/3) × (1/4) ÷ (1/4) = 1/3
3. 3 对贝叶斯公式另外一种理解
其实还有一种对贝爷斯公式的理解和解法,即分类用乘法法分步用加分的概念

3.1 3.1 分类
就是把分类(事件)看成分类,例如:
示例1中的爷爷和奶奶
示例2中的男性和女性
示例3中的各类试题
简单理解就是先验概率P(X)
3.2 3.2 分步
分步可以看成在限定条件下,即在分类范围下的事件发生概率,例如:
示例1中,在爷爷或者奶奶的总红包数量范围下,抽中100元红包的概率
示例2中,在男性或者女性限定条件下,穿凉鞋的概率
示例3中,在回答各类试卷的范围,答对的概率
这里的概率就是条件概率,条件概率的分母只是在所在分类或者范围下,这个分类的汇总总和
条件概率形式上使用P(W | X)或者P(答对 | B类试题)或者P( 男性 | 凉鞋) ,中间为竖线
3.3 3.3 全概率
此时再通过分类用乘法法分步用加分的概念,就是先用分步的思想得出各事件在全局(包含各分类的视觉下)算出全局的概率,就是联合概率
联合概率就是表示两个事件共同发生的概率
计算出同时满足各分类下各事件发生的概率后,再通过分类相加的思想,得出的就是该事件在全局的全概率
提示:在享受本文内容的同时,请注意版权归属 徐州鑫坤机电设备有限公司https://www.xzxkjd.com如果您觉得有价值欢迎分享,但请务必注明出处,感谢您的理解,谢谢!
以下部分内容需要登录查看 立即登录

 简体中文
简体中文 繁體中文
繁體中文 English
English Nederlands
Nederlands Français
Français Русский язык
Русский язык Polski
Polski 日本語
日本語 ภาษาไทย
ภาษาไทย Deutsch
Deutsch Português
Português español
español Italiano
Italiano 한어
한어 Suomalainen
Suomalainen Gaeilge
Gaeilge dansk
dansk Tiếng Việt
Tiếng Việt Pilipino
Pilipino Ελληνικά
Ελληνικά Maori
Maori tongan
tongan ᐃᓄᒃᑎᑐᑦ
ᐃᓄᒃᑎᑐᑦ ଓଡିଆ
ଓଡିଆ Malagasy
Malagasy Norge
Norge bosanski
bosanski नेपालीName
नेपालीName čeština
čeština فارسی
فارسی हिंदी
हिंदी Kiswahili
Kiswahili ÍslandName
ÍslandName ગુજરાતી
ગુજરાતી Slovenská
Slovenská היברית
היברית ಕನ್ನಡ್Name
ಕನ್ನಡ್Name Magyar
Magyar தாமில்
தாமில் بالعربية
بالعربية বাংলা
বাংলা Azərbaycan
Azərbaycan lifiava
lifiava IndonesiaName
IndonesiaName Lietuva
Lietuva Malti
Malti català
català latviešu
latviešu УкраїнськаName
УкраїнськаName Cymraeg
Cymraeg ກະຣຸນາ
ກະຣຸນາ తెలుగుQFontDatabase
తెలుగుQFontDatabase Română
Română Kreyòl ayisyen
Kreyòl ayisyen Svenska
Svenska հայերեն
հայերեն ဗာရမ်
ဗာရမ် پښتوName
پښتوName Kurdî
Kurdî Türkçe
Türkçe български
български Malay
Malay मराठीName
मराठीName eesti keel
eesti keel മലമാലം
മലമാലം slovenščina
slovenščina اوردو
اوردو አማርኛ
አማርኛ ਪੰਜਾਬੀName
ਪੰਜਾਬੀName albanian
albanian Hrvatski
Hrvatski Suid-Afrikaanse Dutch taal
Suid-Afrikaanse Dutch taal ខ្មែរKCharselect unicode block name
ខ្មែរKCharselect unicode block name




